Cho một tấm nhôm hình vuông cạnh 6cm. Người ta muốn cắt một hình thang như hình vẽ. Trong đó AE = 2(
Câu hỏi
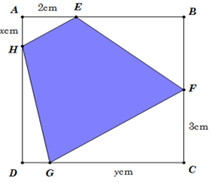
Nhận biếtCho một tấm nhôm hình vuông cạnh (6cm.) Người ta muốn cắt một hình thang như hình vẽ. Trong đó (AE = 2left( {cm} right),AH = xleft( {cm} right),CF = 3left( {cm} right),CG = yleft( {cm} right).) Tìm tổng (x + y) để diện tích hình thang (EFGH) đạt giá trị nhỏ nhất.
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Ta có \({S_{EFGH}} = {S_{ABCD}} - {S_{AEH}} - {S_{BEF}} - {S_{CFG}} - {S_{DGH}}\)
Mà \({S_{ABCD}} = 6.6 = 36;{S_{BEF}} = \dfrac{1}{2}BE.BF = \dfrac{1}{2}.4.3 = 6\) nên \({S_{EFGH}} = 30 - \left( {{S_{\Delta AEH}} + {S_{\Delta CGF}} + {S_{\Delta DGH}}} \right)\)
Do đó \({S_{EFGH}}\) nhỏ nhất \( \Leftrightarrow S = {S_{\Delta AEH}} + {S_{\Delta CGF}} + {S_{\Delta DGH}}\) lớn nhất.
Ta có: \(S = \dfrac{1}{2}AE.AH + \dfrac{1}{2}CF.CG + \dfrac{1}{2}DG.DH\) \( = x + \dfrac{{3y}}{2} + \dfrac{{\left( {6 - x} \right)\left( {6 - y} \right)}}{2}\)
\( \Rightarrow 2S = 2x + 3y + \left( {6 - x} \right)\left( {6 - y} \right)\) \( = xy - 4x - 3y + 36\) \(\left( 1 \right)\)
Ta có \(EFGH\) là hình thang \( \to \) \(\widehat {AEH} = \widehat {CGF}\)
\( \Rightarrow \Delta AEH~\Delta CGF\)\( \Rightarrow \dfrac{{AE}}{{CG}} = \dfrac{{AH}}{{CF}}\) \( \Rightarrow \dfrac{2}{y} = \dfrac{x}{3} \Rightarrow xy = 6\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(2S = 42 - \left( {4x + \dfrac{{18}}{x}} \right)\).
Để \(2S\) lớn nhất khi và chỉ khi \(4x + \dfrac{{18}}{x}\) nhỏ nhất.
Mà \(4x + \dfrac{{18}}{x} \ge 2\sqrt {4x.\dfrac{{18}}{x}} = 12\sqrt 2 .\)
Dấu \('' = ''\) xảy ra \( \Leftrightarrow 4x = \dfrac{{18}}{x} \Leftrightarrow x = \dfrac{{3\sqrt 2 }}{2} \to y = 2\sqrt 2 \).
Chọn C.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.