Một trang trại nuôi gia cầm muốn rào thành hai chuồng hình chữ nhật s
Câu hỏi
Nhận biếtMột trang trại nuôi gia cầm muốn rào thành hai chuồng hình chữ nhật sát nhau và sát một con sông (như hình vẽ), một chuồng vịt và một chuồng ngan. Biết rằng trang trại đã có sẵn 240m hàng rào. Hỏi tổng diện tích lớn nhất của hai chuồng có thể là bao nhiêu?
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
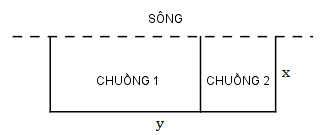
Gọi chiều rộng của mảnh đất là x và chiều dài của mảnh đất là y ta có \(3x+2y=240\Leftrightarrow y=120-\frac{3}{2}x\)
Tổng diện tích của hai chuồng là \(S=xy=x\left( 120-\frac{3}{2}x \right)=-\frac{3}{2}{{x}^{2}}+120x\)
Đồ thị hàm số là một parabol có bề lõm hướng xuống, đạt GTLN tại \(x=-\frac{b}{2a}=-\frac{120}{2.\left( -\frac{3}{2} \right)}=40\), khi đó \(S=-\frac{3}{2}{{.40}^{2}}+120.40=2400{{m}^{2}}\)
Chọn A.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.