Cho chiếc trống như hình vẽ, có đường sinh là nửa elip được cắt bởi tr
Câu hỏi
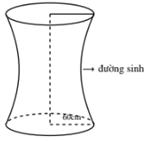
Nhận biếtCho chiếc trống như hình vẽ, có đường sinh là nửa elip được cắt bởi trục lớn với độ dài trục lơn bằng \(80cm,\) độ dài trục bé bằng \(60cm\) . Tính thể tích \(V\) của trống (kết quả làm tròn đến hàng đơn vị)

Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Gắn hệ trục tọa độ như sau :
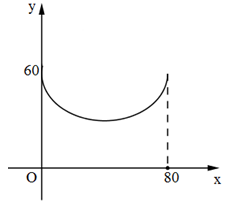
Ta có phương trình Elip : \(\frac{{{{\left( {x - 40} \right)}^2}}}{{{{40}^2}}} + \frac{{{{\left( {y - 60} \right)}^2}}}{{{{30}^2}}} = 1\).
\(\begin{array}{l} \Rightarrow {\left( {y - 60} \right)^2} = {30^2}\left( {1 - \frac{{{{\left( {x - 40} \right)}^2}}}{{{{40}^2}}}} \right)\\ \Leftrightarrow y - 60 = - \frac{3}{4}\sqrt {{{40}^2} - {{\left( {x - 40} \right)}^2}} \\ \Leftrightarrow y = 60 - \frac{3}{4}\sqrt {{{40}^2} - {{\left( {x - 40} \right)}^2}} \end{array}\)
(Do phần đồ thị được lấy nằm phía dưới đường thẳng \(y = 60\))
Khi đó ta có \(V = \pi \int\limits_0^{80} {{{\left( {60 - \frac{3}{4}\sqrt {{{40}^2} - {{\left( {x - 40} \right)}^2}} } \right)}^2}dx} \)
Sử dụng MTCT ta tính được \(V = \)
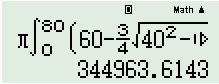
Chọn B.
Luyện tập
Câu hỏi liên quan
-









Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
 =
=  =
=  và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.

 là số thực và z2 =
là số thực và z2 =  là số ảo.
là số ảo.

