Cho hình lập phương ABCD.A'B'C'D’ có cạnh bằng 2. Cắt hình lập phương
Câu hỏi
Nhận biếtCho hình lập phương \(ABCD.A'B'C'D’ \) có cạnh bằng 2. Cắt hình lập phương bằng một mặt phẳng chứa đường chéo AC’. Tìm giá trị nhỏ nhất của diện tích thiết diện thu được.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
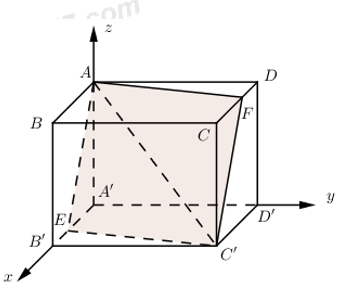
Giả sử mặt phẳng chứa AC’ cắt hình lập phương theo thiết diện là tứ giác AEC’F. \(\left( E\in A'B';F\in CD \right)\)
Ta có:
\(\left\{ \begin{align}\left( AEC'F \right)\cap \left( ABCD \right)=AF \\\left( AEC'F \right)\cap \left( A'B'C'D' \right)=EC' \\\left( ABCD \right)//\left( A'B'C'D' \right) \\\end{align} \right.\Rightarrow AF//EC’\)
Tương tự ta chứng minh được AE // FC’
\(\Rightarrow AEC'F\) là hình bình hành \(\Rightarrow {{S}_{AEC'F}}=2{{S}_{AEC'}}\)
Gắn hệ trục tọa độ như hình vẽ sao cho \(A'\left( 0;0;0 \right);B'\left( 2;0;0 \right);C'\left( 2;2;0 \right);D'\left( 0;2;0 \right);A\left( 0;0;2 \right),B\left( 2;0;2 \right)\), \(C\left( 2;2;2 \right);D\left( 0;2;2 \right)\) .
Gọi \(E\left( x;0;0 \right)\,\,\left( 0\le x\le 2 \right)\) ta có:
\(\overrightarrow{AC'}\left( 2;2;-2 \right);\overrightarrow{AE}=\left( x;0;-2 \right)\Rightarrow {{S}_{AEC'}}=\frac{1}{2}\left| \left[ \overrightarrow{AC'};\overrightarrow{AE} \right] \right|=\frac{1}{2}\sqrt{8\left( {{x}^{2}}-2x+4 \right)}\)
Ta có \({{x}^{2}}-2x+4={{\left( x-1 \right)}^{2}}+3\ge 3\Rightarrow {{S}_{AEC'}}\ge \frac{1}{2}\sqrt{8.3}=\sqrt{6}\)
Dấu bằng xảy ra \(\Leftrightarrow x=1\), khi đó \({{S}_{AEC'\,\,\min }}=\sqrt{6}\Rightarrow {{S}_{AEC'F\,\,\min }}=2\sqrt{6}\)
Chọn D.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.