Cho hàm số y = x3 - 3x2 + 4 (C) 1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (HS tự làm).
Câu hỏi
Nhận biếtCho hàm số y = x3 - 3x2 + 4 (C)
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (HS tự làm).
2. Viết phương trình đường thẳng d cắt đồ thị (C) tại ba điểm phân biệt M(2;0), N, P sao cho tiếp tuyến của (C) tại N và P vuông góc với nhau.
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
1. Khảo sát hàm số y = x3-3x2+4 (C)
+ Tập xác định: D = R
+ Giới hạn: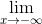 
y = - ∞, 
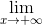y = +∞
+ Đạo hàm y' = 3x2 - 6x; y' = 0 ⇔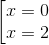 
Bảng biến thiên:
Hàm số đồng biến trên các khoảng (-∞; 0), (2;+∞), nghịch biến trên khoảng (0; 2)
Hàm số đạt cực đại tại x = 0, yCĐ= 4
Hàm số đạt cực tiểu tại x = 2, yCT= 0
+ Đồ thị:
Đồ thị hàm số đi qua điểm (-1;0) và nhận điểm I(1;2) làm tâm đối xứng
2. Phương trình đường thẳng d đi qua điểm M(2; 0) và có hệ số góc k là:
y = k(x - 2)
Phương trình hoành độ giao điểm của (C) và d là: k(x - 2) = x3 - 3x2 + 4
⇔ (x - 2)(x2 - x - 2 - k) = 0 ⇔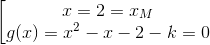 
Đường thẳng d cắt (C) tại 3 điểm phân biệt M, N, P
⇔ Phương trình g(x) = 0 có hai nghiệm phân biệt khác 2
⇔∆ > 0 và g(2) ≠ 0 ⇔ - 
< k ≠ 0 (*).
Theo định lí Viet ta có: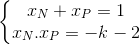 
Các tiếp tuyến tại M, N vuông góc với nhau ⇔ y'(xP).y’(xN) = -1
⇔ (3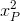
- 6xP)(3
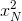- 6xN) = -1
⇔ 9k2 + 18k + 1 = 0 ⇔ k =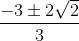 
(thỏa mãn (*))
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
