Cho tam giác ABC đều cạnh Đường thẳng d đi qua A và vuông góc với mặt phẳng ( ABC ). Điểm S thay đổi
Câu hỏi
Nhận biếtCho tam giác \(ABC\) đều cạnh Đường thẳng d đi qua A và vuông góc với mặt phẳng \(\left( {ABC} \right)\). Điểm S thay đổi trên d (S khác A). Gọi H là trực tâm của tam giác SBKhi đó H thuộc một đường tròn cố định, tính đường kính của đường tròn đó.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
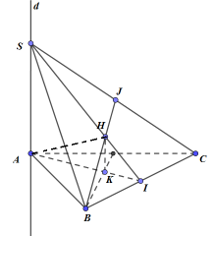
Gọi K là trực tâm của tam giác ABC; I, J lần lượt là chân đường cao của tam giác SBC ứng với đỉnh S, B.
\( \Rightarrow HK//SA \Rightarrow HK \bot \left( {ABC} \right)\)\( \Rightarrow BC \bot HK\) (1)
Ta có: \(\left\{ \begin{array}{l}BK \bot AC\\BK \bot SA\end{array} \right. \Rightarrow BK \bot \left( {SAC} \right) \Rightarrow BK \bot SC\)
Mà \(SC \bot BH \Rightarrow SC \bot \left( {BHK} \right) \Rightarrow SC \bot HK\) (2)
Từ (1), (2) suy ra \(HK \bot \left( {SBC} \right) \Rightarrow HK \bot HI \Rightarrow H\) thuộc mặt cầu (S) có đường kính là IK. (Mặt cầu này là cố định do I, K lần lượt là trung điểm cạnh BC, trực tâm tam giác ABC, đều là các điểm cố định).
Mặt khác H thuộc mặt phẳng cố định là \(\left( \alpha \right)\) (mặt phẳng chứa AI và vuông góc với (ABC).
\( \Rightarrow H \in \left( C \right)\) là đường tròn giao tuyến của \(\left( \alpha \right)\) và \(\left( S \right)\).
Do đường kính \(IK \in \left( \alpha \right)\) nên \(\left( C \right)\) là đường tròn có đường kính bằng đường kính mặt cầu \(\left( S \right)\), có độ dài là:
\(IK = \dfrac{1}{3}.AI = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{6}\).
Chọn: B
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
