Ông An có một khu đất hình elip với độ dài trục lớn 10 m và độ dài trục bé 8 m. Ông An muốn chia khu
Câu hỏi
Nhận biếtÔng An có một khu đất hình elip với độ dài trục lớn 10 m và độ dài trục bé 8 m. Ông An muốn chia khu đất làm 2 phần, phần thứ nhất là một hình chữ nhật nội tiếp elip dùng để xây bể cá cảnh và phần còn lại dùng để trồng ho Biết chi phí xây bể cá là 1 000 000 đồng trên 1\({m^2}\) và chi phí trồng hoa là 1 200 000 đồng trên 1\({m^2}\). Hỏi ông An có thể thiết kế xây dựng như trên với tổng chi phí thấp nhất gần nhất với số nào dưới đây?
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
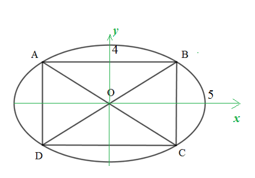
Phương trình đường elip là: \(\dfrac{{{x^2}}}{{25}} + \dfrac{{{y^2}}}{{16}} = 1\,\,\left( E \right)\)
Diện tích khu đất hình elip là: \(S = \pi ab = \pi .5.4 = 20\pi \left( {{m^2}} \right)\)
(Quan sát hình vẽ) Giả sử độ dài đoạn AB là x (m), độ dài đoạn BC là y (m), (x, y > 0).
Do các điểm A, B, C, D nằm trên \(\left( E \right)\) nên ta có:
\(\dfrac{{{{\left( {\dfrac{x}{2}} \right)}^2}}}{{25}} + \dfrac{{{{\left( {\dfrac{y}{2}} \right)}^2}}}{{16}} = 1 \Leftrightarrow \dfrac{{{x^2}}}{{100}} + \dfrac{{{y^2}}}{{64}} = 1 \Leftrightarrow {y^2} = \dfrac{{16\left( {100 - {x^2}} \right)}}{{25}} \Leftrightarrow y = \dfrac{{4\sqrt {100 - {x^2}} }}{5}\)
Diện tích của hình chữ nhật ABCD là: \({S_{ABCD}} = x.y = x.\dfrac{{4\sqrt {100 - {x^2}} }}{5} = \dfrac{{4x\sqrt {100 - {x^2}} }}{5}\left( {{m^2}} \right)\)
Khi đó, số tiền ông An phải trả là:
\(T = \dfrac{{4x\sqrt {100 - {x^2}} }}{5}.1\,000\,000 + \left( {20\pi - \dfrac{{4x\sqrt {100 - {x^2}} }}{5}} \right).1\,200\,000\)
\( = 24\,\,000\,\,000\,\pi - 160\,\,000x\sqrt {100 - {x^2}} \) (đồng)
Ta có: \(x\sqrt {100 - {x^2}} \le \dfrac{{{x^2} + 100 - {x^2}}}{2} = 50\)
\( \Rightarrow 24\,000\,000\pi - 160\,000x\sqrt {100 - {x^2}} \ge 24\,000\,000\pi - 8\,000\,000\)
\( \Rightarrow {T_{\min }} = 240\,000\,000\pi - 8\,000\,000 \approx \)67 398 224 (đồng) khi và chỉ khi \(x = \sqrt {100 - {x^2}} \Leftrightarrow x = 5\sqrt 2 \).
Chọn: A
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.