Ông An xây dựng một sân bóng đá mini hình chữ nhật có chiều rộng 30m và chiều dài 50m. Để giảm bớt c
Câu hỏi
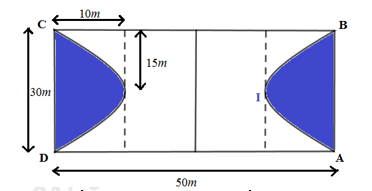
Nhận biếtÔng An xây dựng một sân bóng đá mini hình chữ nhật có chiều rộng 30m và chiều dài 50m. Để giảm bớt chi phí cho việc trồng cây nhân tạo, ông An chia sân bóng ra làm hai phần (tô đen và không tô đen) như hình bên. Phần tô đen gồm hai miền diện tích bằng nhau và đường cong AIB là một parabol đỉnh I. Phần tô đen được trồng có nhân tạo với giá 130 000 đồng/\({m^2}\) và phần còn lại được trồng có nhân tạo với giá 90 000 đồng/\({m^2}\). Hỏi ông An phải trả bao nhiêu tiền để trồng có nhân tạo cho sân bóng?
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
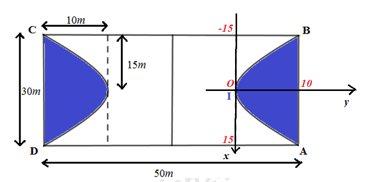
Ta gắn hệ trục Oxy như hình vẽ:
Giả sử phương trình đường Parabol là : \(y = a{x^2} + bx + c,\,\left( {a \ne 0} \right)\).
Ta có: \(\left\{ \begin{array}{l}c = 0\\10 = 225a + 15b\\10 = 225a - 15b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 0\\a = \dfrac{2}{{45}}\\b = 0\end{array} \right.\) \( \Rightarrow \left( P \right):y = \dfrac{2}{{45}}{x^2}\)
Diện tích phần sân tô đậm là:
\(S = 2.\int\limits_{ - 15}^{15} {\dfrac{2}{{45}}{x^2}dx} = \left. {2.\dfrac{2}{{45}}.\dfrac{1}{3}.{x^3}} \right|_{ - 15}^{15} = \left. {\dfrac{4}{{135}}{x^3}} \right|_{ - 15}^{15} = \dfrac{4}{{135}}{.15^3}.2 = 200\,\left( {{m^2}} \right)\)
Diện tích phần còn lại là: \(30.50 - 200 = 1300\,\left( {{m^2}} \right)\)
Ông An phải trả số tiền là: \(200.\,\,130\,\,000\, + 1300.\,\,90\,\,000\, = 26\,000\,000 + 117\,000\,000 = 143\,\,000\,\,000\) (đồng).
Chọn: D
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
