Một biển quảng cáo có dạng hình elip với bốn đỉnh A1A2B1B2 như hình vẽ bên. Biết chi phí để sơn phần
Câu hỏi
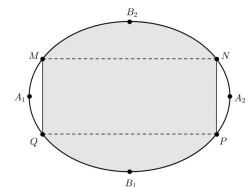
Nhận biếtMột biển quảng cáo có dạng hình elip với bốn đỉnh \({A_1},\,\,{A_2},\,\,{B_1},\,\,{B_2}\) như hình vẽ bên. Biết chi phí để sơn phần tô đậm là 200.000 đồng/ m2 và phần còn lại là 100.000 đồng/m2. Hỏi số tiền để sơn theo cách trên gần nhất với số tiền nào dưới đây, biết \({A_1}{A_2} = 8m,\,\,{B_1}{B_2} = 6m\) và tứ giác MNPQ là hình chữ nhật có \(MQ = 3m\) ?
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
(E) đã cho có độ dài trục lớn \(2a = 8 \Rightarrow a = 4\), độ dài trục bé \(2b = 6 \Rightarrow b = 3\).
Ta có diện tích (E) bằng : \({S_{\left( E \right)}} = \pi .4.3 = 12\pi \,\,\left( {{m^2}} \right)\)
Phương trình \(\left( E \right):\,\,\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1 \Rightarrow {y^2} = 9.\frac{{16 - {x^2}}}{{16}} \Leftrightarrow y = \pm \frac{{3\sqrt {16 - {x^2}} }}{4}\).
Ta có \(M \in \left( E \right);\,\,{y_M} = \frac{1}{2}MQ = \frac{3}{2} \Rightarrow {x_M} = - 2\sqrt 3 \Rightarrow M\left( { - 2\sqrt 3 ;\frac{3}{2}} \right)\)
Diện tích phần giới hạn bởi (E), trục Ox, đường thẳng MQ có diện tích:
\({S_{AMQ}} = 2\int\limits_{ - 4}^{ - 2\sqrt 3 } {\frac{{3\sqrt {16 - {x^2}} }}{4}dx} \approx 1,087 \Rightarrow \) Diện tích phần trắng là: \({S_{trang}} = 2{S_{AMQ}} = 2,174\,\,\left( {{m^2}} \right)\)
Khi đó diện tích phần xanh là \({S_{xanh}} = {S_{\left( E \right)}} - {S_{trang}} = 12\pi - 2,174 = 35,525\,\,\left( {{m^2}} \right)\).
Vậy chi phí để sơn biển quảng cáo là \(2,174.100 + 35,525.200 \approx 7322\) (nghìn đồng) \( \approx 7322000\) đồng.
CHỌN A.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.