Viết ngẫu nhiên một số tự nhiên gồm 5 chữ số phân biệt lên bảng. Tính xác suất để trong số đó có mặt
Câu hỏi
Nhận biếtViết ngẫu nhiên một số tự nhiên gồm 5 chữ số phân biệt lên bảng. Tính xác suất để trong số đó có mặt chữ số 1 và chữ số 3.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Trước hết, ta có số các số gồm 5 chữ số phân biệt là = 27216.
Bây giờ, gọi X là số các số tự nhiên có 5 chữ số phân biệt trong đó có mặt chữ số 1 và chữ số 3.
Để lập nên số có 5 chữ số phân biệt trong đó có mặt chữ số 1 và chữ số 3 ta thực hiện như sau: lấy ra 3 số trong tập 8 chữ số { 0, 2, 4, 5, 6, 7, 8, 9} cùng với chữ số 1 và chữ số 3 rồi sắp xếp 5 chữ số đó theo thứ tự, miễn là số đầu tiên khác chữ số 0.
Do đó : X =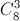 
.5!- 
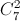. 4!= 6216.
Suy ra xác suất cần tính là P=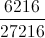 
= 
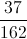≈0,23.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.