Trong không gian Oxyz cho 3 điểm A( 0;1;1 )B( 3;0;-1 )C( 0;21;-19 ) và mặt cầu ( S ):( x-1 )^2+( y-
Câu hỏi
Nhận biếtTrong không gian Oxyz, cho 3 điểm \(A\left( 0;1;1 \right),\,B\left( 3;0;-1 \right),\,C\left( 0;21;-19 \right)\) và mặt cầu \(\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}+{{\left( z-1 \right)}^{2}}=1\). Điểm M thuộc mặt cầu (S) sao cho tổng \(3M{{A}^{2}}+2M{{B}^{2}}+M{{C}^{2}}\) đạt giá trị nhỏ nhất, khi đó, độ dài vectơ \(\overrightarrow{OM}\) là
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
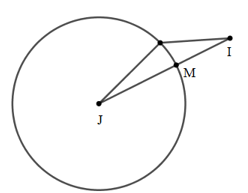
+) Mặt cầu \(\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}+{{\left( z-1 \right)}^{2}}=1\) có tâm \(J\left( 1;1;1 \right)\), bán kính \(R=1\).
+) Tìm \(I\): \(3\overrightarrow{IA}+2\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}\Leftrightarrow 6\overrightarrow{IA}+2\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{0}\Leftrightarrow \overrightarrow{IA}=-\frac{2\overrightarrow{AB}+\overrightarrow{AC}}{6}\)
Ta có: \(A\left( 0;1;1 \right),\,B\left( 3;0;-1 \right),\,C\left( 0;21;-19 \right)\Rightarrow \overrightarrow{IA}\left( -{{x}_{I}};1-{{y}_{I}};1-{{z}_{I}} \right),\,\,\overrightarrow{AB}\left( 3;-1;-2 \right),\,\,\overrightarrow{AC}\left( 0;20;-20 \right)\)
\(\Rightarrow \left\{ \begin{align} & -{{x}_{I}}=-\frac{2.3+0}{6} \\ & 1-{{y}_{I}}=-\frac{2.\left( -1 \right)+20}{6} \\ & 1-{{z}_{I}}=-\frac{2.\left( -2 \right)+\left( -20 \right)}{6} \\\end{align} \right.\Rightarrow I\left( 1;4;-3 \right)\)
+) Ta có:
\(\begin{align} & 3M{{A}^{2}}+2M{{B}^{2}}+M{{C}^{2}}=3{{\left( \overrightarrow{MI}+\overrightarrow{IA} \right)}^{2}}+2{{\left( \overrightarrow{MI}+\overrightarrow{IB} \right)}^{2}}+{{\left( \overrightarrow{MI}+\overrightarrow{IC} \right)}^{2}} \\ & =6M{{I}^{2}}+3I{{A}^{2}}+2I{{B}^{2}}+I{{C}^{2}}+2.\overrightarrow{MI}.\left( 3\overrightarrow{IA}+2\overrightarrow{IB}+\overrightarrow{IC} \right)=6M{{I}^{2}}+3I{{A}^{2}}+2I{{B}^{2}}+I{{C}^{2}}+2.\overrightarrow{MI}.\overrightarrow{0} \\ & =6M{{I}^{2}}+3I{{A}^{2}}+2I{{B}^{2}}+I{{C}^{2}} \\\end{align}\)
Để tổng trên là nhỏ nhất thì MI nhỏ nhất \(\Rightarrow M\)là giao điểm của đoạn thẳng \(IJ\) và mặt cầu \(\left( S \right)\).
\(\overrightarrow{JI}=\left( 0;3;-4 \right)\)
\(\Rightarrow \)Tọa độ điểm \(M\)thuộc đoạn IJ có dạng \(\left( 1;1+3t;1-4t \right),\,\,t\in \left[ 0;1 \right]\)
Mặt khác \(M\in \left( S \right)\Rightarrow {{\left( 1-1 \right)}^{2}}+{{\left( 1-\left( 1+3t \right) \right)}^{2}}+{{\left( 1-\left( 1-4t \right) \right)}^{2}}=1\)
\(\Leftrightarrow {{t}^{2}}=\frac{1}{25}\Leftrightarrow \left[ \begin{align} & t=\frac{1}{5} \\ & t=-\frac{1}{5}\,(L) \\\end{align} \right.\Leftrightarrow t=\frac{1}{5}\) \(\Rightarrow M\left( 1;\frac{8}{5};\frac{1}{5} \right)\Rightarrow OM=\frac{3\sqrt{10}}{5}\).
Chọn: C
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.