Vòm cửa lớn của một trung tâm văn hóa có hình parabol. Người
Câu hỏi
Nhận biếtVòm cửa lớn của một trung tâm văn hóa có hình parabol. Người ta dự định lắp vào cửa kính cho vòm cửa này. Hãy tính diện tích mặt kính cần lắp vào biết rằng vòm cửa cao 8m và rộng 8m.
Đáp án đúng: A
Lời giải của Tự Học 365
Cách giải nhanh bài tập này
Gọi phương trình parabol là \(y = a{x^2} + bx + c\)
Nhận thấy với x = 0 thì y = 8. Suy ra c = 8. Suy ra phương trình parabol có dạng \(y = a{x^2} + bx + 8\).
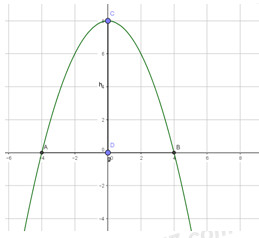
Chiều rộng của parabol bằng 8 nên ta có thể giả sử hình dáng của parabol như hình bên. Khi đó parabol đi qua 2 điểm (4; 0) và (-4; 0).
\( \Rightarrow \left\{ \matrix{ 0 = 16a + 4b + 8 \hfill \cr 0 = 16a - 4b + 8 \hfill \cr} \right. \Rightarrow \left\{ \matrix{ a = - {1 \over 2} \hfill \cr b = 0 \hfill \cr} \right. \Rightarrow y = - {1 \over 2}{x^2} + 8.\)
Bài toán quy về tính diện tích được tạo bởi parabol với trục Ox.
Do có cận đối xứng nên \(S = 2\int\limits_0^4 {\left| { - {{{x^2}} \over 2} + 8} \right|dx} = 2\int\limits_0^4 {\left( { - {{{x^2}} \over 2} + 8} \right)dx} = 2\left. {\left( { - {{{x^3}} \over 6} + 8x} \right)} \right|_0^4 = {{128} \over 3}{m^2}\)
Chọn A.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
