Giải phương trình: (x2-1)
Câu hỏi
Nhận biếtGiải phương trình: (x2-1)![sqrt[3]{2x-1}](http://images.tuyensinh247.com/picture/learning/exam/2014/0109/16832_870284_1.gif)
+x=x![sqrt[3]{(2x-1)^{2}}](http://images.tuyensinh247.com/picture/learning/exam/2014/0109/16832_5186_2.gif)
Đáp án đúng: B
Lời giải của Tự Học 365
Cách giải nhanh bài tập này
(x2-1)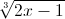
+x=x
Đặt y=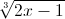
<=> y3=2x-1 <=>y3+1=2x (1)
Thay y=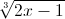 vào phương trình ta được:
(x2-1).y+x=x.y2
<=>x2y-y+x=xy2
<=>(x2y-xy2)+x-y=0
<=>xy(x-y)+(x-y)=0
<=> (x-y)(xy+1)=0
<=>
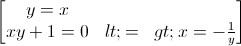
Với y=x thay vào (1)=> x3-2x+1=0
<=>
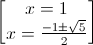
Với x=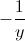
thay vào (1)=>y3+1=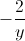
<=>y4+y+2=0 <=> y4-y2+
+y2+y++
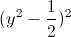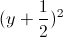=0
<=>
+
+=0
=> Phương trình vô nghiệm
Vậy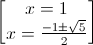
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
