Tìm số nguyên dương n nhỏ nhất sao cho z1 =
Câu hỏi
Nhận biếtTìm số nguyên dương n nhỏ nhất sao cho z1 = 
là số thực và z2 = 
là số ảo.
Đáp án đúng: C
Lời giải của Tự Học 365
Lời giải chi tiết:
Ta có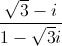 
= 
+ 
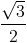i = cos
+isin
Suy ra z1 =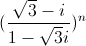 
= 
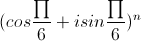= cos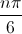
+ isin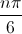
Do đó z1 là số thực ⇔ sin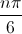 = 0 ⇔ n = 6k, với k nguyên dương.
Ta cũng có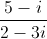 
= 1 + i = √2(cos
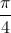+ isin).
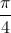Suy ra z2 =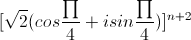 
= √2n+2(cos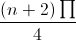
+ isin)
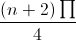Do đó z2 là số ảo ⇔ cos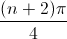
= 0 ⇔ n + 2 = 4l + 2 ⇔ n = 4l, với l nguyên dương.
Từ đó ta suy ra số nguyên dương n nhỏ nhất thỏa mãn bài toán là n = 12.
= 
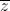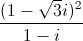. Tìm modun của số phức 
= (
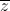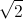+ i)2 (1 -