Tứ diện OABC, OA, OB, OC đôi một vuông góc. H là hình chiếu vuông góc

Câu hỏi
Nhận biếtTứ diện OABC, OA, OB, OC đôi một vuông góc. H là hình chiếu vuông góc của O lên mặt phẳng \(\left( {ABC} \right)\). Chứng minh
a) \(BC \bot \left( {AOH} \right)\)
b) H là trực tâm \(\Delta ABC\).
c) \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
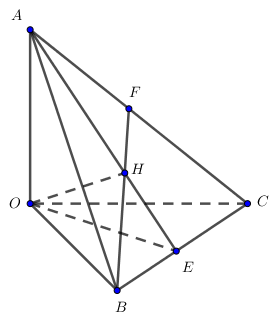
a) * \(OH \bot \left( {ABC} \right) \Rightarrow OH \bot BC\,\,\left( 1 \right)\)
* \(\left\{ \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right. \Rightarrow OA \bot \left( {BOC} \right) \Rightarrow OA \bot BC\,\,\left( 2 \right)\)
* Từ (1) và (2) \( \Rightarrow BC \bot \left( {AOH} \right)\).
b) * Nối \(AH \cap BC = E\). Theo a) ta có :
\(BC \bot \left( {AOH} \right) \Rightarrow BC \bot AH \Rightarrow BC \bot AE\,\,\left( 3 \right)\)
* Chứng minh tương tự ta có \(AC \bot \left( {BOH} \right) \Rightarrow AC \bot BF\,\,\left( 4 \right)\)
* Từ (3) và (4) \( \Rightarrow H\) là trực tâm tam giác ABC.
c) * Tam giác vuông AOE có : \(\frac{1}{{C{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{E^2}}}\,\,\left( 5 \right)\)
* Tam giác vuông BOC có: \(\frac{1}{{O{E^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\,\,\left( 6 \right)\)
* Thay (6) vào (5) có \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\).









