Tứ diện ABCD có AB = AC = AD = a;BAC = BAD = 60^0. a) Chứng minh AB v

Câu hỏi
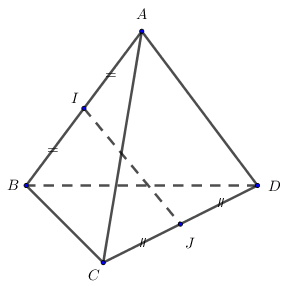
Nhận biếtTứ diện ABCD có \(AB = AC = AD = a;\,\,\widehat {BAC} = \widehat {BAD} = {60^0}\).
a) Chứng minh \(AB \bot CD\)
b) I; J lần lượt là trung điểm của AB, CD. Chứng minh \(IJ \bot AB\).
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
Cách 1: Chứng minh bình thường.
Cách 2: Tham khảo chứng minh bằng vector.
\(\begin{array}{l}a)\,\,\overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow {AB} \left( {\overrightarrow {CA} + \overrightarrow {AD} } \right) = \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AC} \\ = AB.AD.\cos \widehat {BAD} - AB.AC.\cos \widehat {BAC} = 0\\ \Rightarrow \overrightarrow {AB} \bot \overrightarrow {CD} \end{array}\)
b) I; J là trung điểm của AB, CD. Ta có:
\(\overrightarrow {IJ} = \frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {BC} } \right) = \frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {AC} - \overrightarrow {AB} } \right)\)
Ta có \(\overrightarrow {AB} .\overrightarrow {IJ} = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AB} .\overrightarrow {AC} - \overrightarrow {AB} .\overrightarrow {AB} } \right)\)
\(\begin{array}{l} = \frac{1}{2}\left( {AD.AB.\cos {{60}^0} + AB.AC.\cos {{60}^0} - A{B^2}} \right)\\ = \frac{1}{2}\left( {\frac{1}{2}{a^2} + \frac{1}{2}{a^2} - {a^2}} \right) = 0\\ \Rightarrow \overrightarrow {AB} \bot \overrightarrow {IJ} \,\,\left( {dpcm} \right)\end{array}\)









