Tứ diện ABCD, AB vuông góc CD;BC vuông góc AD. Chứng minh AC vuông góc

Câu hỏi
Nhận biếtTứ diện ABCD, \(AB \bot CD;\,\,BC \bot AD\). Chứng minh \(AC \bot BD\).
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
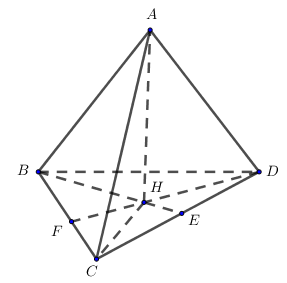
* Vẽ \(AH \bot \left( {BCD} \right)\). Nối
\(BH \cap CD = E;\,\,DH \cap BC = F\).
* \(\left\{ \begin{array}{l}CD \bot AB\\CD \bot AH\end{array} \right. \Rightarrow CD \bot \left( {ABE} \right) \Rightarrow CD \bot BE\,\,\left( 1 \right)\)
* Chứng minh tương tự : \(BC \bot DF\,\,\left( 2 \right)\)
* Từ (1) và (2) \( \Rightarrow H\) là trực tâm tam giác BCD
\( \Rightarrow \left\{ \begin{array}{l}BD \bot CH\\BD \bot AD\end{array} \right. \Rightarrow BD \bot \left( {AHC} \right) \Rightarrow BD \bot AC\).
* Chú ý : Tứ diện này gọi là tứ diện trực tâm.









