Trong mp ( alpha ), cho tứ giác ABCD có AB cắt CD tại E, AC cắt BD tạ

Câu hỏi
Nhận biếtTrong mp \( \left( \alpha \right) \), cho tứ giác \(ABCD \) có \(AB \) cắt \(CD \) tại \(E \), \(AC \) cắt \(BD \) tại \(F \), \(S \) là điểm không thuộc \( \left( \alpha \right) \). Giao tuyến của \( \left( {SAB} \right) \) và \( \left( {SCD} \right) \) là:
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
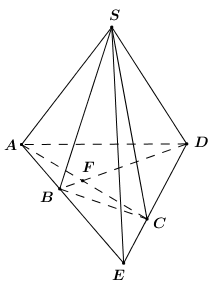
Xét \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\) có:
+ \(S\) là điểm chung thứ nhất.
+ \(AB \cap CD = E \Rightarrow \left\{ \begin{array}{l}E \in AB \subset \left( {SAB} \right)\\E \in CD \subset \left( {SCD} \right)\end{array} \right.\)\( \Rightarrow E \in \left( {SAB} \right) \cap \left( {SCD} \right)\).
Vậy \(\left( {SAB} \right) \cap \left( {SCD} \right) = SE\).
Chọn D.









