Trong mặt phẳng ( P ) cho tứ giác lồi ABCD S là điểm nằm ngoài mặt phẳng ( P ) O là giao điểm của AC

Câu hỏi
Nhận biếtTrong mặt phẳng \(\left( P \right)\) cho tứ giác lồi \(ABCD\), \(S\) là điểm nằm ngoài mặt phẳng \(\left( P \right)\), \(O\) là giao điểm của \(AC\) và \(BD\), \(M\) là trung điểm của \(SC\). Hai đường thẳng nào sau đây cắt nhau ?
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
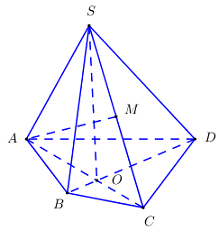
Ta có \(M\) là trung điểm của \(SC \Rightarrow M \in SC \subset \left( {SAC} \right) \Rightarrow M \in \left( {SAC} \right)\).
\( \Rightarrow AM \subset \left( {SAC} \right)\).
\(O = AC \cap BD \Rightarrow O \in AC \subset \left( {SAC} \right) \Rightarrow O \in \left( {SAC} \right)\).
\( \Rightarrow SO \subset \left( {SAC} \right)\).
Do đó \(AM,\,\,SO\) đồng phẳng và không song song, vậy chúng cắt nhau.
Chọn A









