Trong không gian cho hai hình vuông ABCD và ABC'D' có chung cạnh AB và nằm trong hai mặt phẳng khác

Câu hỏi
Nhận biếtTrong không gian cho hai hình vuông \(ABCD\) và \(ABC'D'\) có chung cạnh \(AB\) và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm \(O\) và \(O'\). Hãy xác định góc giữa hai cặp vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {OO'} \)?
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
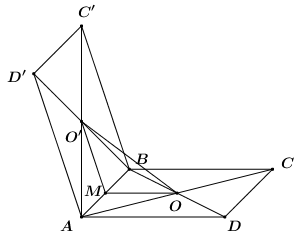
Gọi \(M\) là trung điểm của \(AB\).
Ta có \(OM\) là đường trung bình của tam giác \(ABC\) nên \(OM\parallel BC\).
Mà \(BC \bot AB\) nên \(OM \bot AB\).
CMTT ta có \(O'M \bot AB\).
Ta có:
\(\overrightarrow {OO'} .\overrightarrow {AB} = \left( {\overrightarrow {MO'} - \overrightarrow {MO} } \right).\overrightarrow {AB} \)\( = \overrightarrow {MO'} .\overrightarrow {AB} - \overrightarrow {MO} .\overrightarrow {AB} = 0\).
Vậy \(OO' \bot AB\) hay \(\angle \left( {OO';AB} \right) = {90^0}\).
Chọn D.









