Tính môđun của số phức z biết (1 + 2i)z + (1- 2.<

Câu hỏi
Nhận biếtTính môđun của số phức z biết (1 + 2i)z + (1- 2.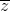 )i = 1 + 3i
)i = 1 + 3i
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Giả sử z = a + bi với a; b ∈ R => 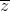 = a - bi
= a - bi
(1 + 2i)z + (1 - 2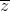 )i = 1 + 3i ⇔ ( 1 + 2i)(a + bi) + (1 - 2(a - bi))i = 1 + 3i
)i = 1 + 3i ⇔ ( 1 + 2i)(a + bi) + (1 - 2(a - bi))i = 1 + 3i
⇔ a + bi + 2ai - 2b + (1 - 2a)i - 2b = 1 + 3i ⇔ a - 4b + ( b + 1) i = 1 + 3i
⇔ 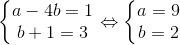
Vậu z = 9 + 2i => |z|= √85

 là số thực và z2 =
là số thực và z2 =  là số ảo.
là số ảo.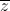 = (
= (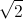 + i)2 (1 -
+ i)2 (1 - 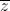 =
= 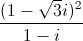 . Tìm modun của số phức
. Tìm modun của số phức