Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm x in [ 0;1 ]. 2sin ^22x1 +
![Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm x in [ 0;1 ].
2sin ^22x1 +](https://tuhoc365.vn/wp-content/uploads/2020/03/qa-238x145.png "Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm x in [ 0;1 ].
2sin ^22x1 +")
Câu hỏi
Nhận biếtTìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm \(x \in \left[ {0;1} \right]\).
\(2{\sin ^2}\frac{{2x}}{{1 + {x^2}}} - \sin \frac{{2x}}{{1 + {x^2}}} - m = 0\).
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Đặt \(u = \frac{{2x}}{{1 + {x^2}}}\). \(x \in \left[ {0;1} \right] \Rightarrow u \in \left[ {0;1} \right]\). Khi đó phương trình trở thành: \(2{\sin ^2}u - \sin u - m = 0\)
Đặt \(t = \sin u;\,\,u \in \left[ {0;1} \right] \Rightarrow t \in \left[ {0;\sin 1} \right]\), phương trình trở thành \(2{t^2} - t - m = 0 \Leftrightarrow 2{t^2} - t = m\,\,\left( * \right)\) (với \(t \in \left[ {0;\sin 1} \right]\)).
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(f\left( t \right) = 2{t^2} - t\) (với \(t \in \left[ {0;\sin 1} \right]\)) và đường thẳng \(y = m\) song song với trục hoành.
Xét hàm số \(f\left( t \right) = 2{t^2} - t\) (với \(t \in \left[ {0;\sin 1} \right]\)) ta có BBT:
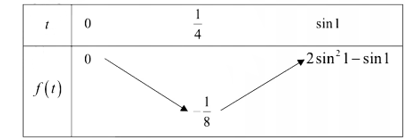
Khi đó phương trình (*) có nghiệm \(t \in \left[ {0;\sin 1} \right] \Leftrightarrow - \frac{1}{8} \le m \le 2{\sin ^2}1 - \sin 1\).
