Tìm tất cả các giá trị của m để phương trình cos 2x - 5sin x + m = 0 có đúng 1 nghiệm thuộc khoảng (

Câu hỏi
Nhận biếtTìm tất cả các giá trị của m để phương trình \(\cos 2x - 5\sin x + m = 0\) có đúng 1 nghiệm thuộc khoảng \(\left( { - \pi ;\frac{\pi }{2}} \right)\).
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Ta có: \(\cos 2x - 5\sin x + m = 0 \Leftrightarrow 1 - 2{\sin ^2}x - 5\sin \,x + m = 0 \Leftrightarrow m = 2{\sin ^2}x + 5\sin x - 1\) (1)
Đặt \(\sin \,x = t\). Khi đó, phương trình (1) trở thành \(m = 2{t^2} + 5t - 1\) (2)
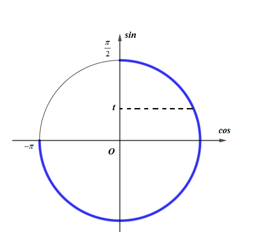
Phương trình (1) có đúng 1 nghiệm thuộc khoảng \(\left( { - \pi ;\frac{\pi }{2}} \right) \Leftrightarrow \)Phương trình (2) có đúng một nghiệm thuộc nửa khoảng \(\left[ {0;1} \right)\)
Xét hàm số \(y = 2{t^2} + 5t - 1,\,\,t \in \left[ {0;1} \right)\), có: \(y' = 4t + 5 > 0,\,\,\forall t \in \left[ {0;1} \right)\)
Bảng biến thiên:
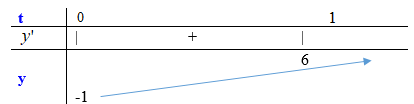
Vậy, phương trình đã cho có đúng 1 nghiệm thuộc khoảng \(\left( { - \pi ;\frac{\pi }{2}} \right)\) khi \( - 1 \le m < 6\).
Chọn: A









