Tìm số phức có modun nhỏ nhất sao cho: |z| = |<

Câu hỏi
Nhận biếtTìm số phức có modun nhỏ nhất sao cho: |z| = |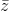 - 3 + 4i|
- 3 + 4i|
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Gọi số phức z có dạng z = x + yi, với x, y ∈ R
Khi đó |z| = |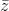 - 3 + 4i|
- 3 + 4i|
⇔ |x + yi| = |x – yi – 3 + 4i| ⇔ |x + yi| = |x – 3 + (4 – y)i|
⇔ x2 + y2 = (x – 3)2 + (4 – y)2 ⇔ 6x + 8y = 25. <=> y = 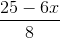
|z| = 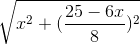 =
= 
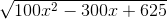 ≥
≥ 
Số phức z có modun nhỏ nhất đạt được khi x =  và y = 2
và y = 2
Vậy z =  + 2i
+ 2i

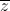 = (
= (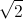 + i)2 (1 -
+ i)2 (1 -  là số thực và z2 =
là số thực và z2 =  là số ảo.
là số ảo.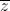 =
= 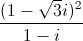 . Tìm modun của số phức
. Tìm modun của số phức