Nghiệm của phương trình cot x - tan x + 4sin 2x = 2sin 2x khi biểu diễn trên đường tròn lượng giác

Câu hỏi
Nhận biếtNghiệm của phương trình \(\cot x - \tan x + 4\sin 2x = \frac{2}{{\sin 2x}}\) khi biểu diễn trên đường tròn lượng giác gồm bao nhiêu điểm khác nhau?
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Điều kiện: \(\sin 2x \ne 0 \Leftrightarrow \cos 2x \ne 1 \Leftrightarrow x \ne \frac{{k\pi }}{2}\,,\,\;k \in \mathbb{Z}\)
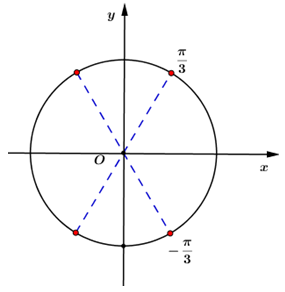
\(\begin{array}{l}\,\,\,\,\,\,\,\frac{{\cos x}}{{\sin x}} - \frac{{\sin x}}{{\cos x}} + 4\sin 2x = \frac{2}{{\sin 2x}}\\ \Leftrightarrow \frac{{{{\cos }^2}x - {{\sin }^2}x}}{{\sin x.\cos x}} + 4\sin 2x = \frac{2}{{\sin 2x}}\\ \Leftrightarrow \frac{{2\cos 2x}}{{\sin 2x}} + 4\sin 2x = \frac{2}{{\sin 2x}}\\ \Leftrightarrow \cos 2x + 2{\sin ^2}2x = 1\\ \Leftrightarrow \cos 2x + 2 - 2{\cos ^2}2x - 1 = 0\\ \Leftrightarrow 2{\cos ^2}2x - \cos 2x - 1 = 0 \Leftrightarrow \left[ \begin{array}{l}\cos 2x = 1\;\;\;\left( {ktm} \right)\\\cos 2x = - \frac{1}{2}\;\;\left( {tm} \right)\end{array} \right.\,\,\,\,\\ \Leftrightarrow \left[ \begin{array}{l}2x = \frac{{2\pi }}{3} + k2\pi \\2x = - \frac{{2\pi }}{3} + m2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k\pi \\x = - \frac{\pi }{3} + m\pi \end{array} \right.\;\left( {k,\;m \in \mathbb{Z}} \right)\,\,.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}\)\(\)\(\)
Với các nghiệm trên biểu diễn bởi 4 điểm trên đường tròn lượng giác.
Chọn B.









