Lăng trụ ABCA’B’C’. G1,G2 là trọng tâm tam giác B’BC và tam giác B’BA.

Câu hỏi
Nhận biếtLăng trụ ABCA’B’C’. \({{G}_{1}},\,{{G}_{2}}\) là trọng tâm tam giác B’BC và tam giác B’BA. Chứng minh \({{G}_{1}}{{G}_{2}}\parallel A'C'\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
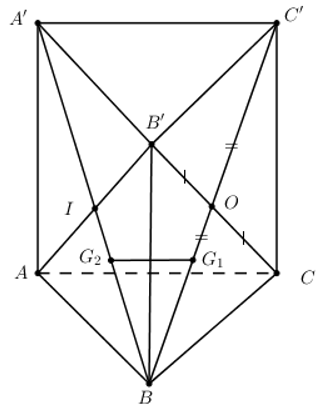
+) Nối \(BC'\cap B'C=O\Rightarrow \) O là trung điểm của BC’ và B’C.
+) \({{G}_{1}}\) là trọng tâm tam giác B’BC \(\Rightarrow \frac{B{{G}_{1}}}{BO}=\frac{2}{3}\Rightarrow \frac{B{{G}_{1}}}{BC'}=\frac{1}{3}\,\left( 1 \right)\)
+) Chứng minh tương tự ta có: \(\frac{B{{G}_{2}}}{BA'}=\frac{1}{3}\,\left( 2 \right)\)
+) Từ (1), (2) \(\Rightarrow \frac{B{{G}_{1}}}{BC'}=\frac{B{{G}_{2}}}{BA'}\Rightarrow {{G}_{1}}{{G}_{2}}\parallel A'C\)









