Hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại A; AB = 1; AC = 2. Hình chiếu vuông góc

Câu hỏi
Nhận biếtHình lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(A;{\rm{ }}AB = 1;{\rm{ }}AC = 2.\) Hình chiếu vuông góc của \(A'\) trên \(\left( {ABC} \right)\) nằm trên đường thẳng \(BC\). Tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {A'BC} \right)\).
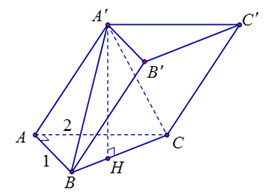
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
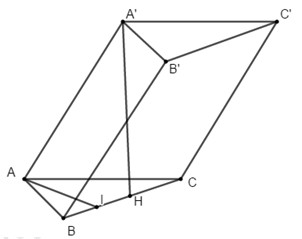
Kẻ \(AI \bot BC\,\,\left( {I \in BC} \right)\).
Lại có \(A'H \bot \left( {ABC} \right) \Rightarrow A'H \bot AI\).
\( \Rightarrow AI \bot \left( {A'BC} \right) \Rightarrow d\left( {A;\left( {A'BC} \right)} \right) = AI\).
Áp dụng hệ thức lượng trong tam giác vuông \(ABC\) ta có:
\(\begin{array}{l} \Rightarrow \dfrac{1}{{A{I^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}} = \dfrac{1}{{{1^2}}} + \dfrac{1}{{{2^2}}}\\ \Leftrightarrow \dfrac{1}{{A{I^2}}} = \dfrac{5}{4} \Leftrightarrow AI = \dfrac{{2\sqrt 5 }}{5}\end{array}\)
Vậy \(d\left( {A;\left( {A'BC} \right)} \right) = \dfrac{{2\sqrt 5 }}{5}\).
Chọn D.









