Gọi alpha beta gamma lần lượt là góc giữa các đường thẳng OAOBOC với mặt phẳng ( ABC ). Tìm giá trị

Câu hỏi
Nhận biếtGọi \(\alpha ,\,\beta ,\,\gamma \) lần lượt là góc giữa các đường thẳng \(OA,\,OB,\,OC\) với mặt phẳng \(\left( {ABC} \right)\). Tìm giá trị lớn
nhất của biểu thức \(P = \cos \alpha + cos\beta + cos\gamma \).
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
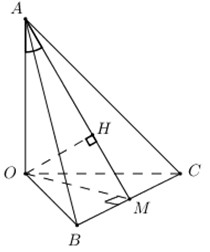
Trong \(\left( {OBC} \right)\) kẻ \(OM \bot BC\), trong \(\left( {OAM} \right)\) kẻ \(OH \bot AM\) ta có:
\(\left\{ \begin{array}{l}BC \bot OM\\BC \bot OA\end{array} \right. \Rightarrow BC \bot \left( {OAM} \right) \Rightarrow BC \bot OH\).
Lại có \(OH \bot AM \Rightarrow OH \bot \left( {ABC} \right)\)
\(\begin{array}{l} \Rightarrow \angle \left( {OA;\left( {ABC} \right)} \right) = \angle \left( {OA;HA} \right) = \angle OAH = \alpha \\\,\,\,\,\,\,\angle \left( {OB;\left( {ABC} \right)} \right) = \angle \left( {OB;HB} \right) = \angle OBH = \beta \\\,\,\,\,\,\angle \left( {OC;\left( {ABC} \right)} \right) = \angle \left( {OC;HC} \right) = \angle OCH = \gamma \end{array}\)
Ta có: \(\sin \alpha = \dfrac{{OH}}{{OA}};\,\,\sin \beta = \dfrac{{OH}}{{OB}};\,\,\sin \gamma = \dfrac{{OH}}{{OC}}\)
\( \Rightarrow {\sin ^2}\alpha + {\sin ^2}\beta + {\sin ^2}\gamma = O{H^2}\left( {\dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}} \right)\)
Áp dụng hệ thức lượng trong tam giác vuông OBC ta có \(\dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}} = \dfrac{1}{{O{M^2}}}\).
Áp dụng hệ thức lượng trong tam giác vuông OAM ta có:
\(\dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{M^2}}} = \dfrac{1}{{O{H^2}}} \Rightarrow \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}} = \dfrac{1}{{O{H^2}}}\)
\( \Rightarrow {\sin ^2}\alpha + {\sin ^2}\beta + {\sin ^2}\gamma = O{H^2}\left( {\dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}} \right) = O{H^2}.\dfrac{1}{{O{H^2}}} = 1\).
Áp dụng BĐT Bunhiacopxki ta có:
\(\begin{array}{l}{P^2} = {\left( {P = \cos \alpha + cos\beta + cos\gamma } \right)^2} \le \left( {{1^2} + {1^2} + {1^2}} \right)\left( {{{\cos }^2}\alpha + co{s^2}\beta + co{s^2}\gamma } \right)\\ \Rightarrow {P^2} \le 3\left[ {3 - \left( {{{\sin }^2}\alpha + {{\sin }^2}\beta + {{\sin }^2}\gamma } \right)} \right] = 3\left[ {3 - 1} \right] = 6\\ \Leftrightarrow - \sqrt 6 \le P \le \sqrt 6 \end{array}\)
Vậy \({P_{\max }} = \sqrt 6 \). Dấu “=” xảy ra \( \Leftrightarrow \cos \alpha = \cos \beta = \cos \gamma = \dfrac{{\sqrt 6 }}{3}\).









