Có bao nhiêu giá trị nguyên của m nhỏ hơn 2018 để phương trình 3sin ^2

Câu hỏi
Nhận biếtCó bao nhiêu giá trị nguyên của m nhỏ hơn 2018 để phương trình \( \dfrac{3}{{{{ \sin }^2}x}} + 3{ \tan ^2}x + \tan x + \cot x = m \) có nghiệm?
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Hướng dẫn giải chi tiết
\(\begin{array}{l}\dfrac{3}{{{{\sin }^2}x}} + 3{\tan ^2}x + \tan x + \cot x = m\\ \Leftrightarrow 3\left( {1 + {{\cot }^2}x} \right) + 3{\tan ^2}x + \tan x + \cot x = m\\ \Leftrightarrow 3\left( {{{\tan }^2}x + {{\cot }^2}x} \right) + \left( {\tan x + \cot x} \right) = m - 3\end{array}\)
Đặt
\(\eqalign{
& t = \tan x + \cot x \Rightarrow {t^2} = {\tan ^2}x + {\cot ^2}x + 2 \Leftrightarrow {t^2} - 2 = {\tan ^2}x + {\cot ^2}x \cr
& {t^2} = {\tan ^2}x + {\cot ^2}x + 2 \ge 2\sqrt {{{\tan }^2}x{{\cot }^2}x} + 2 = 2 + 2 = 4 \Leftrightarrow \left[ \matrix{
t \ge 2 \hfill \cr
t \le - 2 \hfill \cr} \right. \cr}\)
Khi đó phương trình trở thành \(3\left( {{t^2} - 2} \right) + t = m - 3 \Leftrightarrow 3{t^2} + t - 3 = m\)
Xét hàm số \(f\left( t \right) = 3{t^2} + t - 3\) với \(t \in \left( { - \infty ; - 2} \right] \cup \left[ {2; + \infty } \right)\) ta có BBT:
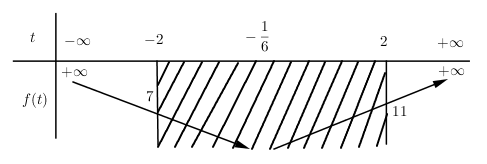
Dựa vào BBT ta thấy để phương trình có nghiệm thỏa mãn yêu cầu bài toán \( \Leftrightarrow m \geqslant 7\)
Vậy \(\left\{ \begin{array}{l}7 \le m < 2018\\m \in Z\end{array} \right. \Rightarrow \) Có \(\left( {2017 - 7} \right) + 1 = 2011\) giá trị của m.
Chọn D.









