Chứng minh rằng BC vuông góc AM và AM vuông góc ( SBC ).

Câu hỏi
Nhận biếtChứng minh rằng \(BC \bot AM\) và \(AM \bot \left( {SBC} \right){\rm{.}}\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
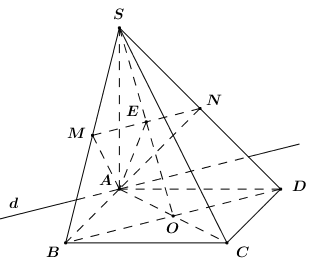
Ta có: \(\left\{ \begin{array}{l}BC \bot AB\,\,\left( {gt} \right)\\BC \bot SA\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\end{array} \right.\) \( \Rightarrow BC \bot \left( {SAB} \right)\).
Mà \(AM \subset \left( {SBC} \right)\) nên \(BC \bot AM\).
Ta có: \(SA \bot \left( {ABCD} \right)\) nên \(SA \bot AB \Rightarrow \Delta SAB\) vuông tại \(A\).
Lại có \(SA = AB = a\) nên \(\Delta SAB\) vuông cân tại \(A\).
\( \Rightarrow \) Trung tuyến \(AM\) đồng thời là đường cao \( \Rightarrow AM \bot SB\).
Lại có \(AM \bot BC\,\,\left( {cmt} \right)\).
Vậy \(AM \bot \left( {SBC} \right)\).









