Chứng minh MN song song với mặt phẳng ( SBC ).

Câu hỏi
Nhận biếtChứng minh \(MN\) song song với mặt phẳng \(\left( {SBC} \right)\).
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
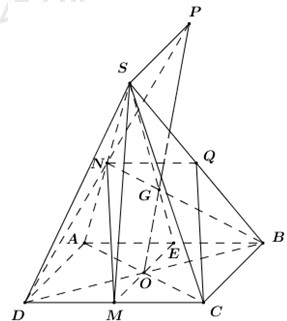
Gọi \(Q\) là trung điểm của \(SB\).
\(NQ\) là đường trung bình của tam giác \(SAB \Rightarrow NQ\parallel AB\) và \(NQ = \dfrac{1}{2}AB\).
\( \Rightarrow NQ\parallel MC\) và \(NQ = MC \Rightarrow MNQC\) là hình bình hành (dhnb).
\( \Rightarrow MN\parallel QC\). Mà \(QC \subset \left( {SAB} \right)\).
Vậy \(MN\parallel \left( {SAB} \right)\).









