Chóp SABCD. Mthuộc SC. a) Tìm giao điểm H của SD và mặt phẳng (MAB)

Câu hỏi
Nhận biếtChóp SABCD. \(M\in SC.\)
a) Tìm giao điểm H của SD và mặt phẳng (MAB)
b) Giả sử \(AB\cap CD=K.\) Chứng minh rằng M, H, K thẳng hàng.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
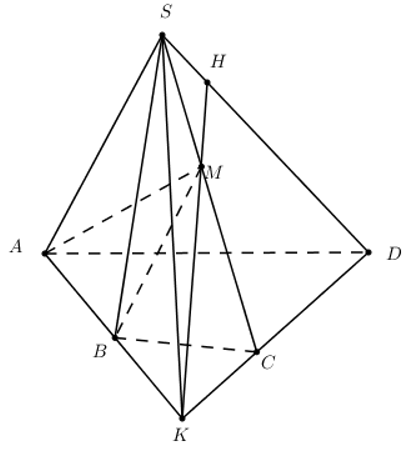
a) +) Bước 1: Cho \(SD\subset \left( SCD \right)\)
+) Bước 2: Nối
\(AB\cap CD=K\Rightarrow \left( MAB \right)\cap \left( SCD \right)=MK\)
+) Bước 3: Nối \(MK\cap SD=H\Rightarrow H\) là giao điểm.
b)
\(\begin{align} & +)\,\,M,\,H,\,K\in \left( SCD \right)\,\,\left( 1 \right) \\ & +)\,\,M,\,H,\,K\in \left( MAB \right)\,\left( 2 \right) \\\end{align}\)
+) Từ (1) và (2) Þ M, H, K thẳng hàng.









