Cho tứ diện SABC có hai mặt ( ABC ) và ( SBC ) là hai tam giác đều cạnh aSA=a căn 32. Gọi M là điểm

Câu hỏi
Nhận biếtCho tứ diện \(SABC\) có hai mặt \(\left( ABC \right)\) và \(\left( SBC \right)\) là hai tam giác đều cạnh \(a,\,\,\,SA=\frac{a\sqrt{3}}{2}.\) Gọi \(M\) là điểm trên \(AB\) sao cho \(AM=b\text{ }\left( 0
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
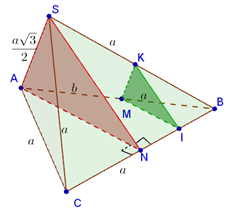
Gọi N là trung điểm của BC.
Ta có
\(\left\{ \begin{array}{l}
SB = SC\\
AB = AC
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
BC \bot SN\\
BC \bot AN
\end{array} \right. \Rightarrow BC \bot \left( {SAN} \right).\)
Theo bài ra \(BC\bot \left( P \right)\Rightarrow \left\{ \begin{align} & M\in \left( P \right) \\ & \left( P \right)//\left( SAN \right) \\\end{align} \right.\).
Kẻ \(MI//AN,\,MK//SA\Rightarrow \) Thiết diện của \(\left( P \right)\) và \(S.ABC\) là \(\Delta KMI.\)
Mà \(\left\{ \begin{align} & \Delta ABC \\ & \Delta SBC \\\end{align} \right.\) là hai tam giác đều cạnh \(a\Rightarrow AN=SN=\frac{a\sqrt{3}}{2}=SA\Rightarrow \Delta SAN\) là tam giác đều cạnh
\(\frac{a\sqrt{3}}{2}\Rightarrow \Delta KMI\) là tam giác đều cạnh \(\frac{\sqrt{3}}{2}.\frac{a-b}{a}\Rightarrow {{S}_{\Delta KMI}}=\frac{3\sqrt{3}}{16}.{{\left( \frac{a-b}{a} \right)}^{2}}.\)
Chọn C









