Cho tứ diện S.ABC có SA vuông góc với mặt phẳng ( ABC ) và tam giác ABC đều. Xác định mặt cắt của tứ

Câu hỏi
Nhận biếtCho tứ diện \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(\left( ABC \right)\) và tam giác \(ABC\) đều. Xác định mặt cắt của tứ diện \(S.ABC\) và mặt phẳng \(\left( \alpha \right)\) qua \(B\) và vuông góc với \(SC.\)
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
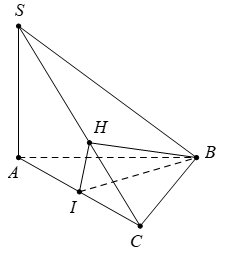
Kẻ BH vuông góc với \(SC\,\,\,\,\,\,\left( H\in SC \right).\)
Gọi I là trung điểm của AC. Ta có \(BI\bot AC\) (do \(\Delta \,ABC\) đều).
Và BI vuông góc với SA (do \(SA\bot mp\,\,\left( ABC \right)\)).
\(\Rightarrow \,\,BI\bot mp\,\,\left( SAC \right)\Rightarrow \,\,BI\bot SC.\) Từ \(\left( 1 \right),\,\,\left( 2 \right)\,\,:\,\,SC\bot mp\,\,\left( BIH \right).\)
Vậy mặt cắt là tam giác BIH vuông tại I.
Chọn B









