Cho tứ diện đều SABC. Gọi I là trung điểm của AB, M là một điểm di động trên đoạn AI. Gọi (P) là mặt

Câu hỏi
Nhận biếtCho tứ diện đều SABC. Gọi I là trung điểm của AB, M là một điểm di động trên đoạn AI. Gọi (P) là mặt phẳng qua M và song song với (SIC). Thiết diện tạo bởi (P) và tứ diện S.ABC là:
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
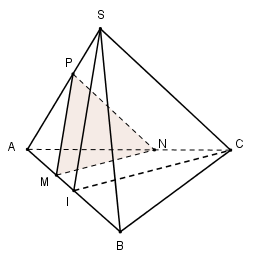
Trong (ABC) qua M kẻ đường thẳng song song với CI cắt AC tại N \(\Rightarrow \left( \alpha \right)\cap \left( ABC \right)=MN\).
Trong (SAB) qua M kẻ đường thẳng song song với SI cắt SA tại P \(\Rightarrow \left( \alpha \right)\cap \left( SAB \right)=MP.\)
\(\Rightarrow \left( \alpha \right)\cap \left( SAC \right)=NP\) và NP // SC.
Vậy thiết diện cần tìm là tam giác MNP.
Ta có: \(ME\parallel CI\Rightarrow \frac{MN}{CI}=\frac{AM}{AI}\Leftrightarrow \frac{MN}{\frac{AB\sqrt{3}}{2}}=\frac{x}{\frac{AB}{2}}\Leftrightarrow MN=\frac{\frac{AB\sqrt{3}}{2}x}{\frac{AB}{2}}=x\sqrt{3}.\)
\(\begin{array}{l}MP\parallel SI \Rightarrow \frac{{MP}}{{SI}} = \frac{{AM}}{{AI}} = \frac{{AP}}{{AS}} \Leftrightarrow \frac{{MP}}{{\frac{{AB\sqrt 3 }}{2}}} = \frac{x}{{\frac{{AB}}{2}}} \Rightarrow MP = \frac{{\frac{{AB\sqrt 3 }}{2}x}}{{\frac{{AB}}{2}}} = x\sqrt 3 \PN\parallel SC \Rightarrow \frac{{AP}}{{AS}} = \frac{{PN}}{{SC}} \Rightarrow \frac{{PN}}{{SC}} = \frac{{AM}}{{AI}} \Leftrightarrow \frac{{PN}}{{SC}} = \frac{x}{{\frac{{AB}}{2}}} \Leftrightarrow PN = \frac{{xSC}}{{\frac{{AB}}{2}}} = 2x\,\,\left( {SC = AB} \right)\end{array}\)
Tam giác MNP có MN = MP nên tam giác MNP cân tại M
Chọn C.









