Cho tứ diện đều ABCD có các cạnh bằng a điểm M trên cạnh AB sao cho AM = m (0 < m < a). Khi đó diện

Câu hỏi
Nhận biếtCho tứ diện đều ABCD có các cạnh bằng a, điểm M trên cạnh AB sao cho AM = m (0 < m < a). Khi đó diện tích của thiết diện của hình tứ diện khi cắt bởi mp\(\left( \alpha \right)\)đi qua M và song song với (ACD) là:
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
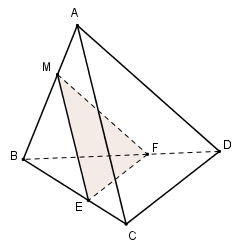
Trong (ABC) qua M kẻ đường thẳng song song với AC cắt BC tại E \(\Rightarrow \left( \alpha \right)\cap \left( ABC \right)=ME\).
Trong (ABD) qua M kẻ đường thẳng song song với AD cắt BD tại F \(\Rightarrow \left( \alpha \right)\cap \left( ABD \right)=MF.\)
\(\Rightarrow \left( \alpha \right)\cap \left( BCD \right)=EF.\)
Vậy thiết diện cần tìm là tam giác MEF.
Ta có: \(ME\parallel CD\Rightarrow \frac{ME}{CD}=\frac{BM}{AB}\Leftrightarrow \frac{ME}{a}=\frac{a-m}{a}\Leftrightarrow ME=a-m.\)
\(\text{EF}\parallel CD\Rightarrow\frac{EF}{CD}=\frac{BE}{BC}=\frac{ME}{AC}\Leftrightarrow \frac{EF}{a}=\frac{a-m}{a}\Rightarrow EF=a-m\).
Chứng minh tương tự ta có MF = a – m.. Suy ra tam giác MEF đều cạnh a – m.
Vậy \({{S}_{MEF}}=\frac{{{\left( a-m \right)}^{2}}\sqrt{3}}{4}.\)
Chọn B.









