Cho tứ diện đều ABCD cạnh a=12 gọi ( P ) là mặt phẳng qua B và vuông góc với AD. Thiết diện của ( P

Câu hỏi
Nhận biếtCho tứ diện đều \(ABCD\) cạnh \(a=12,\) gọi \(\left( P \right)\) là mặt phẳng qua \(B\) và vuông góc với \(AD.\) Thiết diện của \(\left( P \right)\) và hình chóp có diện tích bằng
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
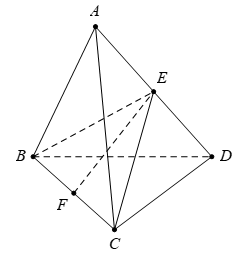
Gọi E là trung điểm của AD ta có \(BE\bot AD,CE\bot AD\Rightarrow AD\bot \left( BCE \right)\Rightarrow \left( P \right)\equiv \left( BCD \right)\)
Thiết diện là tam giác BCE.
Gọi F là trung điểm của BC.
Ta có \(BE=CE=\frac{12\sqrt{3}}{2}=6\sqrt{3};\,\,EF=\sqrt{B{{E}^{2}}-B{{F}^{2}}}=6\sqrt{2}\).
Diện tích thiết diện là \(S=\frac{1}{2}EF.BC=\frac{1}{2}.6\sqrt{2}.12=36\sqrt{2}\).
Chọn A.









