Cho tứ diện ABCD. P Q lần lượt là trung điểm của AB CD. Điểm R nằm trên cạnh BC sao cho BR = 2RC. Gọ

Lời giải của Tự Học 365

Giải chi tiết:

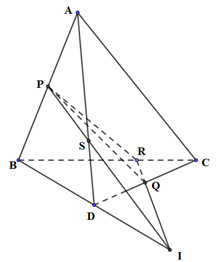
Trong (BCD) gọi I là giao điểm của RQ và BD.

Trong (ABD) gọi S là giao điểm của AD và IP

Khi đó, \(S = AD \cap \left( {PQR} \right)\)

*) Chứng mình D là trung điểm của BI:

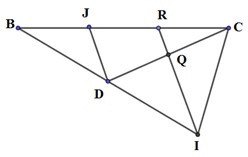
Gọi J là trung điểm của BR. Do R nằm trên cạnh BC sao cho BR = 2RC  \( \Rightarrow BJ = JR = RC\)

Ta có:  \(RQ\) là đường trung bình của tam giác JCD \( \Rightarrow RQ//JD\,\, \Rightarrow RI//JD\)

Xét tam giác BRI có: J là trung điểm của BR, \(DJ//RI \Rightarrow D\) là trung điểm của BI.

*) Xét tam giác ABI có: \(P,D\) lần lượt là trung điểm của AD, BI

\(PI \cap AD = S \Rightarrow S\) là trọng tâm tam giác ABI \( \Rightarrow SA = 2SD\).

Chọn: B