Cho tứ diện ABCD M là trung điểm của cạnh CD G là trọng tâm tứ diện. Khi đó 2 đường thẳng AD và GM l

Câu hỏi
Nhận biếtCho tứ diện ABCD, M là trung điểm của cạnh CD, G là trọng tâm tứ diện. Khi đó 2 đường thẳng AD và GM là hai đường thẳng:
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
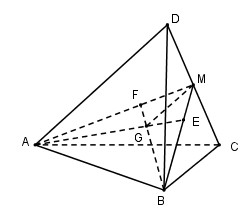
Gọi M là trung điểm của CD, E và F lần lượt là trọng tâm tam giác BCD và ACD \(\Rightarrow E \in BM,F \in AM.\)
Trong (AMB): \(G = AE \cap BF \Rightarrow \) G là trọng tâm của tứ diện ABCD.
Giả sử bốn điểm A, D, G, M đồng phẳng.
A, D, M \( \in \left( {ACD} \right) \Rightarrow G \in \left( {ACD} \right) \Rightarrow AG \subset \left( {ACD} \right) \Rightarrow E \in \left( {ACD} \right)\) (Vô lí)
Do đó A, D, M, G không đồng phẳng.
Vậy AD và GM là hai đường thẳng chéo nhau.
Chọn A.









