Cho tứ diện ABCD. Gọi O là một điểm nằm bên trong tam giác BCD và M là một điểm trên đoạn AO. Gọi IJ

Câu hỏi
Nhận biếtCho tứ diện \(ABCD\). Gọi \(O\) là một điểm nằm bên trong tam giác \(BCD\) và \(M\) là một điểm trên đoạn \(AO\). Gọi \(I,\,\,J\) là hai điểm trên cạnh \(BC,\,\,BD\). Giả sử \(IJ\) cắt \(CD\) tại \(K\), \(BO\) cắt \(IJ\) tại \(E\) và cắt \(CD\) tại \(H\), \(ME\) cắt \(AH\) tại \(F\). Giao tuyến của hai mặt phẳng \(\left( {MIJ} \right)\) và \(\left( {ACD} \right)\) là đường thẳng:
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
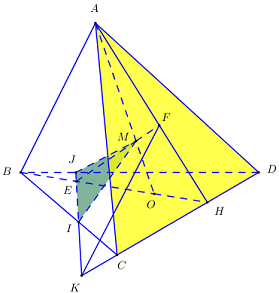
Trong \(\left( {MIJ} \right)\) kéo dài \(ME\) cắt \(AH\) tại \(F\).
Ta có \(F = AH \cap ME \Rightarrow \left\{ \begin{array}{l}F \in AH \subset \left( {SCD} \right)\\F \in ME \subset \left( {MIJ} \right)\end{array} \right.\)
\( \Rightarrow F \in \left( {SCD} \right) \cap \left( {MIJ} \right)\).
Ta có \(\left\{ \begin{array}{l}K \in IJ \subset \left( {MIJ} \right)\\K \in CD \subset \left( {SCD} \right)\end{array} \right. \Rightarrow K \in \left( {MIJ} \right) \cap \left( {SCD} \right)\).
Vậy \(\left( {MIJ} \right) \cap \left( {SCD} \right) = KF\).
Chọn D









