Cho tứ diện ABCD. Gọi M N P lần lượt là trung điểm của AB BC CD. Thiết diện của tứ diện cắt bởi mp(M

Câu hỏi
Nhận biếtCho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của AB, BC, CD. Thiết diện của tứ diện cắt bởi mp(MNP) là hình gì trong các hình sau?
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
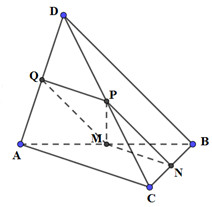
Gọi Q là trung điểm của AD.
Ta có: \(PQ//AC\) (do PQ là đường trung bình của tam giác ACD)
\(MN//AC\) (do MN là đường trung bình của tam giác ABC)
\( \Rightarrow PQ//MN \Rightarrow M,N,P,Q\) đồng phẳng \( \Rightarrow Q \in \left( {MNP} \right)\)
\( \Rightarrow \) Thiết diện của tứ diện cắt bởi mặt phẳng (MNP) là tứ giác MNQP
Ta có: \(PQ//MN,\,\,PQ = MN\left( { = \dfrac{1}{2}AC} \right) \Rightarrow MNQP\) là hình bình hành
Vậy, thiết diện của tứ diện cắt bởi mp(MNP) là hình bình hành.
Chọn: D









