Cho tứ diện ABCD. G là trọng tâm tam giác BCD M là trung điểm CD I là điểm trên đoạn AG BI cắt mặt p

Câu hỏi
Nhận biếtCho tứ diện ABCD. G là trọng tâm tam giác BCD, M là trung điểm CD, I là điểm trên đoạn AG, BI cắt mặt phẳng (ACD) tại J. Khẳng định nào sau đây sai?
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
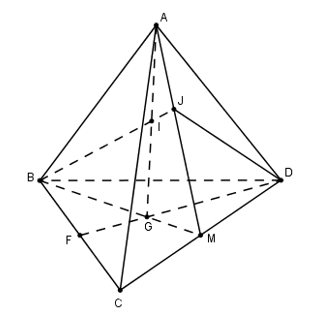
Ta có: \(J \in BI \Rightarrow J \in \left( {ABG} \right);\,\,M \in BG \Rightarrow M \in \left( {ABG} \right)\)
\( \Rightarrow A;J;M\) vừa thuôc mặt phẳng \(\left( {ABG} \right)\), vừa thuộc mặt phẳng \(\left( {ACD} \right)\)
Do đó A; J; G thuộc giao tuyến của hai mặt phẳng (ABG) và (ACD) \( \Rightarrow A;J;G\) thẳng hàng.
\( \Rightarrow \) Đáp án A đúng.
\(AM = \left( {ACD} \right) \cap \left( {ABG} \right) \Rightarrow \) C đúng.
\(DJ = \left( {ACD} \right) \cap \left( {BDJ} \right) \Rightarrow D\) đúng.
Chọn đáp án B.









