Cho tứ diện ABCD đều gọi G là trọng tâm tam giác BCD. Mệnh đề nào sau đây SAI?

Câu hỏi
Nhận biếtCho tứ diện ABCD đều, gọi G là trọng tâm tam giác BCD. Mệnh đề nào sau đây SAI?
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
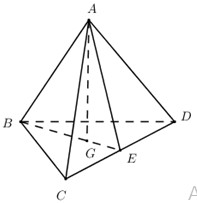
Do \(AB = AC = AD \Rightarrow \) Hình chiếu của A trên \(\left( {BCD} \right)\) trùng với tâm đường tròn ngoại tiếp \(\Delta BCD\).
\(\Delta BCD\) đều \( \Rightarrow G\) là trọng tâm đồng thời là tâm đường tròn ngoại tiếp \(\Delta BCD\).
\( \Rightarrow AG \bot \left( {BCD} \right) \Rightarrow \) Đáp án C đúng.
Gọi E là trung điểm của \(CD\) ta có \(\left\{ \begin{array}{l}CD \bot BE\\CD \bot AG\,\,\left( {AG \bot \left( {BCD} \right)} \right)\end{array} \right. \Rightarrow CD \bot \left( {ABE} \right) \Rightarrow CD \bot AB\).
Giả sử tứ diện \(BCD\) đều cạnh \(a\). Tam giác \(BCD\) đều cạnh \(a \Rightarrow BE = \dfrac{{a\sqrt 3 }}{2}\).
\( \Rightarrow BG = \dfrac{2}{3}BE = \dfrac{{a\sqrt 3 }}{2}\dfrac{2}{3} = \dfrac{{a\sqrt 3 }}{3}\).
Xét tam giác vuông \(ABG\) ta có \(\cos \angle ABG = \dfrac{{BG}}{{AB}} = \dfrac{{\dfrac{{a\sqrt 3 }}{3}}}{a} = \dfrac{{\sqrt 3 }}{3}\).
Do đó đáp án A đúng, đáp án D sai.
Chọn D.









