Cho tứ diện ABCD có M, N theo thứ tự là trung điểm của AB, BC. Gọi P l

Câu hỏi
Nhận biếtCho tứ diện ABCD có M, N theo thứ tự là trung điểm của AB, BC. Gọi P là điểm thuộc cạnh CD sao cho \(CP = 2PD \) và Q là điểm thuộc cạnh AD sao cho bốn điểm M, N, P, Q đồng phẳng. Khẳng định nào sau đây là đúng?
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
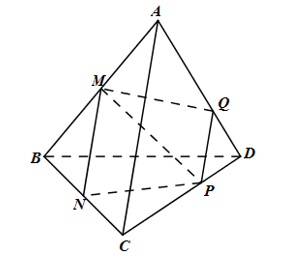
Xét mặt phẳng \(\left( {MNP} \right)\) và mặt phẳng \(\left( {ACD} \right)\) có:
P chung
\(MN \subset \left( {MNP} \right);\,\,AC \subset \left( {ACD} \right);\,\,MN//AC\) (do MN là đường trung bình của tam giác ABC)
\( \Rightarrow \) Giao tuyến của hai mặt phẳng \(\left( {MNP} \right)\) và \(\left( {ACD} \right)\) là đường thẳng qua P và song song với AC.
Trong \(\left( {ACD} \right)\) kẻ \(PQ//AC\,\,\left( {Q \in AD} \right)\), khi đó M, N, P, Q đồng phẳng.
Áp dụng định lí Ta-lét ta có: \(\frac{{AQ}}{{DQ}} = \frac{{CP}}{{DP}} = 2 \Rightarrow AQ = 2DQ\)
Chọn đáp án C.









