Cho tứ diện ABCD có hai cặp cạnh đối vuông góc. Cắt tứ diện đó bằng một mặt phẳng song song với một

Câu hỏi
Nhận biếtCho tứ diện \(ABCD\) có hai cặp cạnh đối vuông góc. Cắt tứ diện đó bằng một mặt phẳng song song với một cặp cạnh đối diện của tứ diện. Trong các mệnh đề sau mệnh đề nào đúng?
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
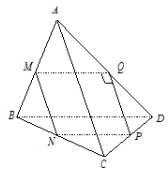
Giả sử cắt tứ diện đó bằng một mặt phẳng song song với \(BD,\,\,AC\).
Giả sử thiết diện là \(MNPQ\).
Ta có: \(\left\{ \begin{array}{l}\left( {MNPQ} \right) \cap \left( {ABD} \right) = MQ\\\left( {MNPQ} \right) \cap \left( {BCD} \right) = NP\\\left( {ABD} \right) \cap \left( {BCD} \right) = BD\end{array} \right. \Rightarrow MQ\parallel NP\parallel BD\).
CMTT ta có \(MN\parallel PQ\parallel AC\).
\( \Rightarrow MNPQ\) là hình bình hành.
Lại có \(AC \bot BD\,\,\left( {gt} \right)\) nên \(MN \bot MQ\).
Vậy tứ giác \(MNPQ\) là hình chữ nhật.
Chọn A.









