Cho tam giác ABC. Gọi B’ C’ lần lượt là trung điểm của AB AC. Tam giác ABC biến thành tam giác AB’C’

Câu hỏi
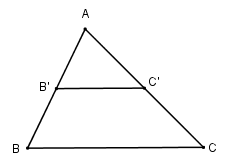
Nhận biếtCho tam giác ABC. Gọi B’ C’ lần lượt là trung điểm của AB, AC. Tam giác ABC biến thành tam giác AB’C’ trong phép vị tự nào?
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Ta có:
x \(\begin{array}{l}\overrightarrow {AB'} = \frac{1}{2}\overrightarrow {AB} \Rightarrow {V_{\left( {A;\frac{1}{2}} \right)}}\left( B \right) = B'\\\overrightarrow {AC'} = \frac{1}{2}\overrightarrow {AC} \Rightarrow {V_{\left( {A;\frac{1}{2}} \right)}}\left( C \right) = C'\\{V_{\left( {A;\frac{1}{2}} \right)}}\left( A \right) = A.\\ \Rightarrow {V_{\left( {A;\frac{1}{2}} \right)}}\left( {ABC} \right) = AB'C'.\end{array}\)
Chọn C.









