Cho ngũ giác đều ABCDE tâm O biết OA = a . Phép quay Q( Cpi ) biến A thành A’ biến B thành B’. Độ d

Câu hỏi
Nhận biếtCho ngũ giác đều ABCDE tâm O, biết OA = a . Phép quay \({Q_{\left( {C,\pi } \right)}}\) biến A thành A’, biến B thành B’. Độ dài đoạn A’B’ là:
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
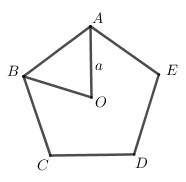
\({Q_{\left( {C;\pi } \right)}}\left( A \right) = A',\,\,{Q_{\left( {C;\pi } \right)}}\left( B \right) = B' \Rightarrow {Q_{\left( {C;\pi } \right)}}\left( {AB} \right) = A'B' \Rightarrow A'B' = AB\)
Xét tam giác cân OAB có \(\widehat {AOB} = {{{{360}^0}} \over 5} = {72^0}\)
Áp dụng định lí Cosin ta có :
\(\eqalign{ & A{B^2} = O{A^2} + O{B^2} - 2.OA.OB.\cos \widehat {AOB} \cr & \,\,\,\,\,\,\,\,\,\, = {a^2} + {a^2} - 2{a^2}.\cos {72^0} = 2{a^2}\left( {1 - \cos {{72}^0}} \right) = 2{a^2}.2{\sin ^2}{36^0} = 4{a^2}{\sin ^2}{36^0} \cr & \Rightarrow AB = 2a\sin {36^0} \Rightarrow A'B' = 2a\sin {36^0} \cr} \)
Chọn D.









