Cho lăng trụ tam giác ABC.A'B'C'. Gọi I,K,G lần lượt là trọng tâm các

Câu hỏi
Nhận biếtCho lăng trụ tam giác \(ABC.A'B'C'.\) Gọi \(I,K,G\) lần lượt là trọng tâm các tam giác \(ABC,\,\,ACC',\,\,A'B'C'.\) Chứng minh \(IK\parallel \left( {ABC'} \right)\,\,;\,\,GK\parallel \left( {BB'C'C} \right)\).
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
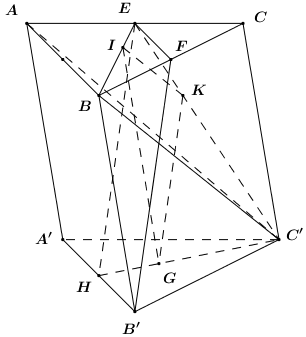
Gọi \(E\) là trung điểm của \(AC\) ta có:
\(\frac{{EI}}{{EB}} = \frac{{EK}}{{EC}} = \frac{1}{3}\) (tính chất trọng tâm) \( \Rightarrow IK\parallel BC'\) (Định lí Ta-lét đảo).
Mà \(BC' \subset \left( {ABC'} \right) \Rightarrow IK\parallel \left( {ABC'} \right)\).
Gọi \(H,\,\,F\) lần lượt là trung điểm của \(A'B'\) và \(BC\).
Ta có: \(\frac{{C'K}}{{C'E}} = \frac{{C'G}}{{C'H}} = \frac{2}{3}\) (Tính chất trọng tâm).
\( \Rightarrow KG\parallel HE\) (Định lí Ta-lét đảo) (1).
Ta có: \(EF\) là đường trung bình của tam giác \(ABC\).
\( \Rightarrow EF\parallel AB\) và \(EF = \frac{1}{2}AB\) (Tính chất đường trung bình)
\( \Rightarrow EF\parallel HB'\) và \(EF = HB'\).
\( \Rightarrow EFB'H\) là hình bình hành \( \Rightarrow HE\parallel B'F\) (2).
Từ (1) và (2) \( \Rightarrow KG\parallel B'F\), mà \(B'F \subset \left( {BCC'B'} \right)\).
Vậy \(KG\parallel \left( {BCC'B'} \right)\).









