Cho hình vuông ABCD trong đó A( 1;1 )B( - 1;1 )C( - 1; - 1 )D( 1; - 1 ). Xét phép quay Q( O;pi 4

Câu hỏi
Nhận biếtCho hình vuông ABCD trong đó \(A\left( {1;1} \right),B\left( { - 1;1} \right),C\left( { - 1; - 1} \right),D\left( {1; - 1} \right)\). Xét phép quay \(Q\left( {O;{\pi \over 4}} \right)\). Giả sử hình vuông A’B’C’D’ là ảnh của ABCD qua phép quay đó. Gọi S là diện tích hình vuông A’B’C’D’ nằm ngoài hình vuông ABCD. Tính S.
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
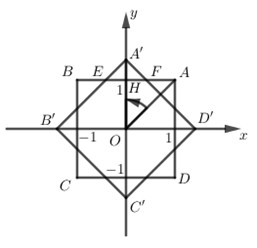
\({Q_{\left( {O;{\pi \over 4}} \right)}}\left( A \right) = A',{Q_{\left( {O;{\pi \over 4}} \right)}}\left( B \right) = B',{Q_{\left( {O;{\pi \over 4}} \right)}}\left( C \right) = C',{Q_{\left( {O;{\pi \over 4}} \right)}}\left( D \right) = D'\) như hình vẽ.
Ta có: \(OA' = OA = \sqrt 2 \Rightarrow A'H = \sqrt 2 - 1\)
Dễ thấy tam giác A’EF là tam giác vuông cân tại A’ \( \Rightarrow EF = 2A'H = 2\left( {\sqrt 2 - 1} \right)\)
\( \Rightarrow {S_{\Delta A'EF}} = {1 \over 2}A'H.EF = {1 \over 2}\left( {\sqrt 2 - 1} \right).2\left( {\sqrt 2 - 1} \right) = {\left( {\sqrt 2 - 1} \right)^2}\)
Vậy diện tích hình vuông A’B’C’D’ nằm ngoài hình vuông ABCD là \(S = 4{\left( {\sqrt 2 - 1} \right)^2} = 4\left( {3 - 2\sqrt 2 } \right) = 12 - 8\sqrt 2 \)
Chọn B.









