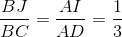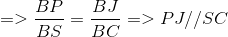Cho hình thang ABCD có AB // CD và S không thuộc mặt phẳng (ABCD) . Tr
Câu hỏi
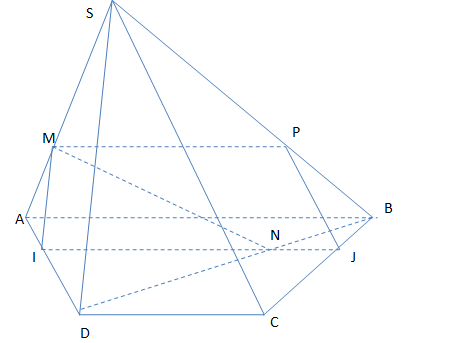
Nhận biếtCho hình thang ABCD có AB // CD và S không thuộc mặt phẳng (ABCD) . Trên SA ; BD lấy 2 điểm M , N sao cho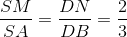 
. Kẻ NI // AB ( I 
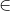AD) .
a) Chứng minh : MI // (SBD) ; (MNI) // (SCD) . Suy ra MN // (SCD)
b) Tìm P 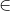(MNI) SB . Chứng minh PJ // SC
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
a) Ta có :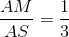 
Do NI // AB nên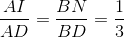 
Suy ra :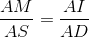 
=> MI // SD => MI // (SBD)
Do NI // AB => NI // CD
Vậy (MNI) // (SCD) nên MN // (SCD)
b) Trong mặt phẳng (ABCD) ta có : NI 
BC = {J}
Do AB // IJ suy ra (SAB) cắt (IMN) theo giao tuyến MP và MP // AB // IJ
Vậy P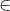 
SB (MNI)
Ta có : MP // AB do đó :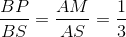 
IJ // AB do đó : 
